Atomic Mass Unit: Unlocking the Secrets of Matter

The atomic mass unit (amu) is a crucial concept in chemistry and physics, allowing scientists to measure atomic and molecular masses with precision. This article examines the history, definition, and applications of the atomic mass unit, examining its significance in scientific studies. The atomic mass unit is also explored in the context of isotopic variation and the relationship between atomic mass and molar mass. Key concepts such as unified atomic mass units (u) and the role of carbon-12 as a standard are discussed, providing a thorough understanding of this fundamental unit in modern science.

Introduction to the Atomic Mass Unit (AMU)

The atomic mass unit (amu) is a standard unit used to express the masses of atoms, molecules, and subatomic particles. As atoms are extremely small, their masses are also minuscule, and measuring them using standard units such as grams or kilograms would be impractical. The amu allows scientists to quantify atomic mass with precision, forming the basis of atomic theory and molecular studies.

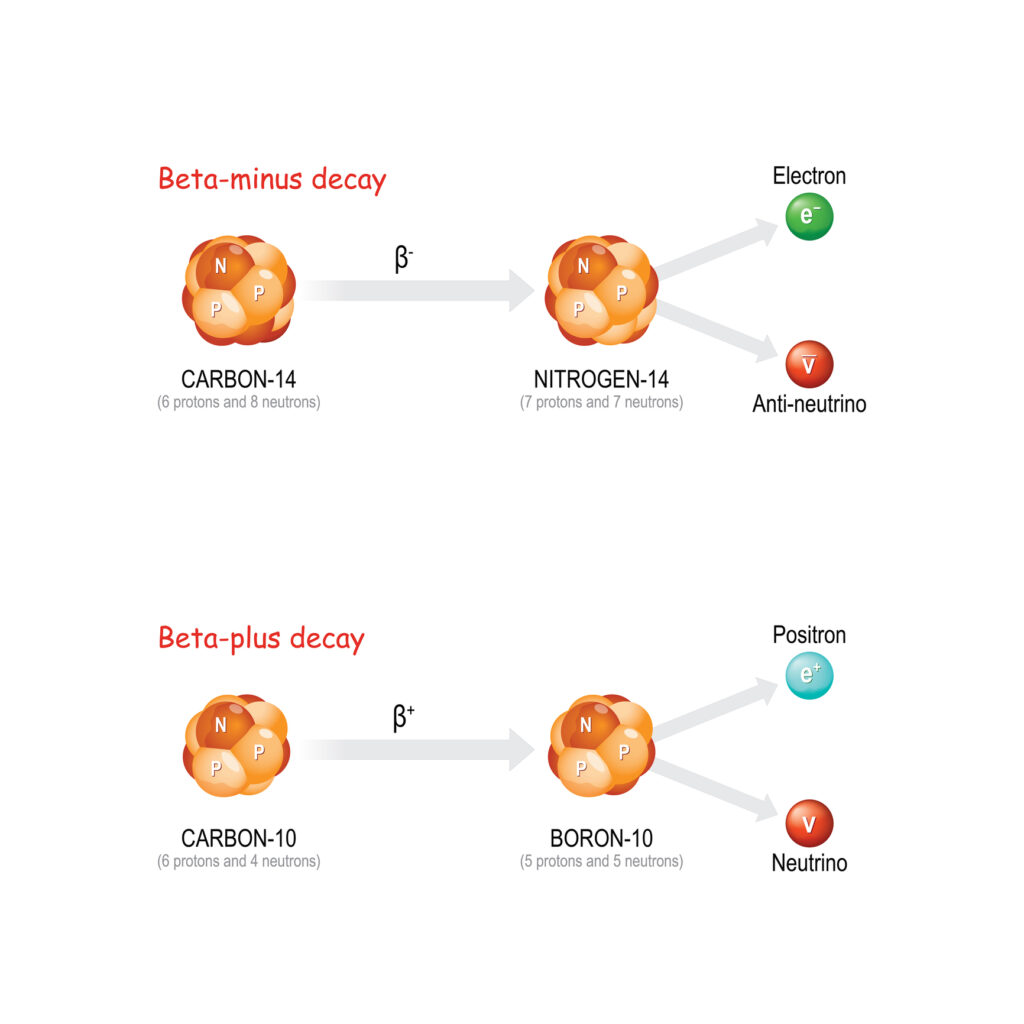
The amu is also referred to as the unified atomic mass unit (u), a name adopted after 1961 to standardise the unit globally. Prior to this, two different scales based on hydrogen and oxygen were used. Today, the carbon-12 isotope is the standard reference for the atomic mass unit, facilitating uniformity in scientific calculations.

Historical Development of the Atomic Mass Unit

The concept of an atomic mass unit has evolved significantly over time. Initially, scientists used the lightest element, hydrogen, as a reference. However, early in the 20th century, oxygen became the standard due to its abundance and easy availability. The introduction of isotopic data revealed discrepancies between hydrogen-based and oxygen-based scales, which led to confusion within the scientific community.

In 1961, an international agreement established the carbon-12 isotope as the definitive reference for the atomic mass unit. Carbon-12 was chosen because it is a stable isotope and widely used in organic chemistry and biology. According to this standard, one atomic mass unit is defined as one-twelfth of the mass of a carbon-12 atom.

Definition and Calculation of the Atomic Mass Unit

The atomic mass unit is defined as one-twelfth of the mass of a carbon-12 atom, which equates to approximately 1.66053906660×10^-27 kilograms. In terms of energy, this mass corresponds to approximately 931.494 MeV/c² (mega-electronvolts per speed of light squared).

Using Einstein’s mass-energy equivalence.

E = mc²

We know that 1 amu = 1/12th the mass of an atom of carbon-12.

1 amu = 1.67 x 10^-27 Kg

Now substitute this in the mass-energy equivalence equation.

E = 1.67 x 10^-27 Kg x (3 x 10⁸)² J

E = 1.67 x 10^-27 Kg x (3 x 10⁸)² J / 1.6 x 10^-19

E = 931 Mev

1 eV = 1.6 x 10^-19 J

Hence, it proved that 1 amu = 931.5 MeV

This relationship is essential in nuclear physics, where mass-energy equivalence is a central principle.

To calculate the atomic mass of an element, scientists use the weighted average of the isotopic masses of that element. For example, chlorine exists primarily as two isotopes: chlorine-35 and chlorine-37. By considering the natural abundance of each isotope, scientists determine the relative atomic mass of chlorine, which is approximately 35.45 amu.

The amu is indispensable for expressing the masses of individual atoms or isotopes and for comparing elements. These calculations are crucial in various scientific fields, such as chemistry, physics, and biology, where accurate measurements of atomic and molecular masses are essential.

The Unified Atomic Mass Unit (u)

In modern contexts, the atomic mass unit is referred to as the unified atomic mass unit, denoted by the symbol ‘u.’ The introduction of this term standardised the use of atomic mass units in both chemistry and physics, ensuring consistency across international research. The use of the carbon-12 isotope as the universal reference established a reliable and reproducible standard for the scientific community.

One of the key benefits of the unified atomic mass unit is its precision. It enables scientists to measure the mass of subatomic particles, such as protons and neutrons, with great accuracy. A proton’s mass is approximately 1.007 u, while a neutron’s mass is around 1.009 u. The slight difference in mass between these particles plays a critical role in the structure and behaviour of atomic nuclei.

Atomic Mass and Molar Mass

The atomic mass unit is intricately connected to the concept of molar mass, which is the mass of one mole of a substance. A mole is a fundamental unit in chemistry, defined as 6.022×10²³ particles (Avogadro’s number). Molar mass is expressed in grams per mole (g/mol) and is numerically equivalent to the atomic or molecular mass in amu. For example, carbon has an atomic mass of approximately 12 amu, and its molar mass is 12 g/mol.

This relationship between atomic mass and molar mass is critical in chemical reactions, where scientists often work with macroscopic quantities of substances. By knowing the molar mass, chemists can calculate the number of atoms or molecules in a given sample, facilitating stoichiometric calculations in reaction equations.

Isotopic Variations and Atomic Mass

Most elements exist in nature as mixtures of isotopes—atoms with the same number of protons but different numbers of neutrons. The atomic mass listed for each element on the periodic table is the weighted average of the masses of its naturally occurring isotopes. This explains why atomic masses are often non-integer values.

For example, carbon has two stable isotopes: carbon-12 and carbon-13. Carbon-12 is the most abundant isotope, comprising about 98.9% of all carbon atoms, while carbon-13 makes up the remaining 1.1%. The atomic mass of carbon is therefore slightly higher than 12 amu (approximately 12.011 u) due to the presence of carbon-13. Understanding isotopic variation is vital in fields such as radiochemistry, geochemistry, and environmental science, where isotopic signatures provide insights into natural processes.

Applications of the Atomic Mass Unit

The atomic mass unit has a wide range of applications in various scientific disciplines. In chemistry, it plays a central role in calculating molecular masses, which are crucial for understanding the composition and behaviour of substances. The atomic mass of each element helps chemists predict how different substances will react and combine in a chemical reaction.

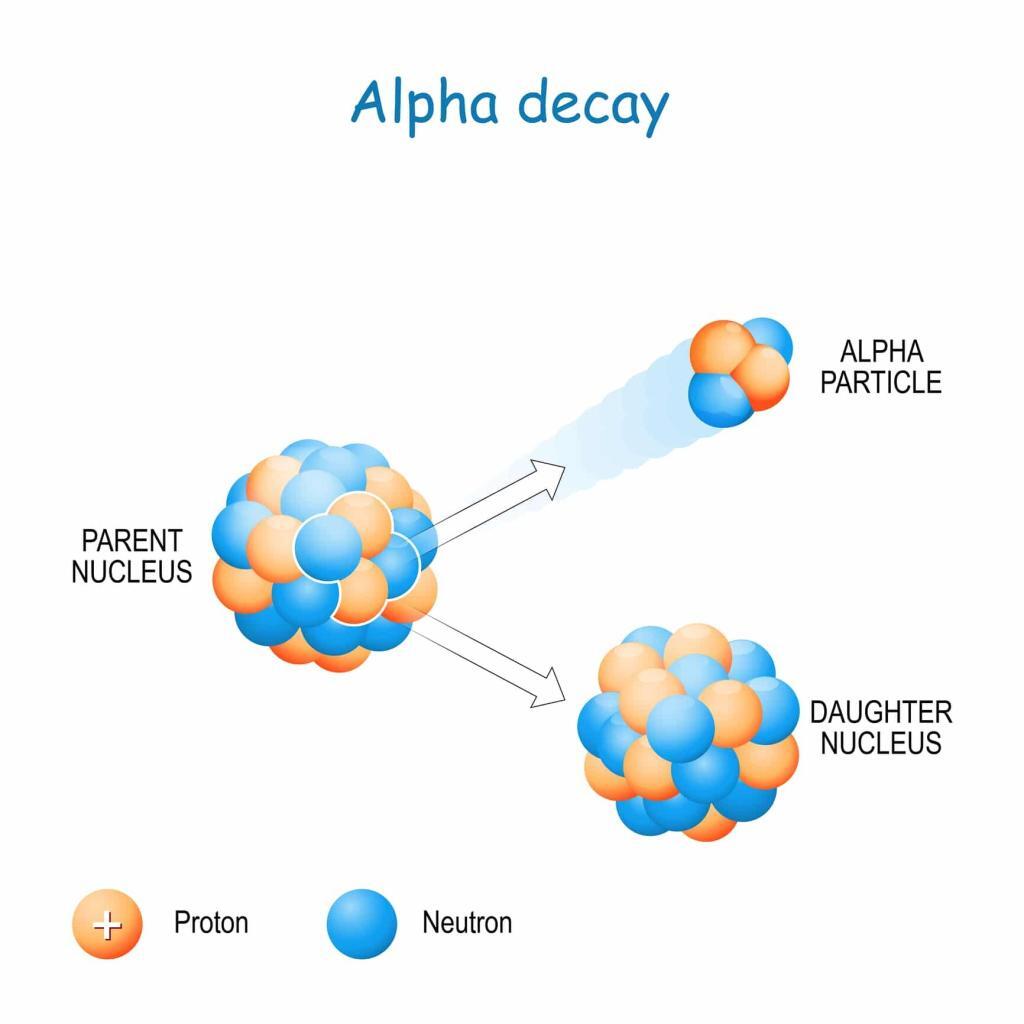
In nuclear physics, the atomic mass unit is fundamental for measuring the masses of atomic nuclei and calculating the energy released in nuclear reactions. The famous equation E=mc² demonstrates the relationship between mass and energy, where the slight differences in atomic masses result in significant amounts of energy during nuclear fission or fusion.

In biology and biochemistry, molecular masses measured in atomic mass units are critical for understanding the structure and function of biomolecules such as proteins, DNA, and RNA. Mass spectrometry, a technique widely used to identify and characterise biomolecules, relies on precise measurements of molecular masses in amu.

Mass Spectrometry and the Atomic Mass Unit

Mass spectrometry is a powerful analytical technique that measures the mass-to-charge ratio (m/z) of ions. It is commonly used in chemistry, biology, and materials science to identify and quantify compounds, study molecular structures, and characterise complex mixtures. The atomic mass unit is the standard for expressing the masses of ions in a mass spectrum, facilitating comparisons between different samples.

In mass spectrometry, molecules are ionised, and their ions are accelerated in an electric field. The mass-to-charge ratio of each ion is determined by its velocity and the strength of the magnetic field. By analysing the resulting mass spectrum, scientists can identify the components of a sample and determine their molecular masses with high precision.

The atomic mass unit is essential for interpreting mass spectra, where the relative abundance of isotopes can be observed. This technique is particularly useful in isotope ratio analysis, where the isotopic composition of a sample can reveal information about its origin, history, or environmental conditions.

Challenges and Limitations of the Atomic Mass Unit

While the atomic mass unit is an invaluable tool for measuring atomic and molecular masses, it does have limitations. The accuracy of atomic mass measurements depends on the precision of the experimental techniques used. Small uncertainties in isotopic abundances or instrumental calibration can lead to slight variations in atomic mass values.

Additionally, the atomic mass unit is less useful when dealing with very large molecules, such as proteins or polymers, where the molecular mass may exceed hundreds of thousands of atomic mass units. In these cases, scientists often use the dalton (Da), a unit equivalent to the atomic mass unit, to express the mass of large biomolecules.

Another challenge arises in high-energy physics, where the masses of subatomic particles such as quarks are extremely small and difficult to measure directly. In these contexts, the atomic mass unit is less commonly used, and other units such as electronvolts (eV) or giga-electronvolts (GeV) are preferred.

The Future of Atomic Mass Measurements

As scientific research advances, new techniques and technologies are being developed to improve the precision and accuracy of atomic mass measurements. The development of highly sensitive mass spectrometers, for example, has allowed scientists to measure atomic masses with unprecedented accuracy, facilitating discoveries in fields ranging from medicine to cosmology.

The International Union of Pure and Applied Chemistry (IUPAC) continues to update the atomic masses of elements as new data becomes available, ensuring that the periodic table reflects the latest scientific knowledge. In the future, further refinements to the atomic mass unit and its application may arise as our understanding of atomic structure and subatomic particles deepens.

Conclusion

The atomic mass unit is a fundamental concept in the study of atomic and molecular masses. By providing a standard for measuring the incredibly small masses of atoms and subatomic particles, the atomic mass unit has become an indispensable tool in chemistry, physics, and biology. From the early adoption of hydrogen and oxygen scales to the modern use of carbon-12 as a reference, the atomic mass unit has undergone significant refinement to ensure precision and consistency in scientific calculations.

The unified atomic mass unit (u) allows scientists to accurately determine the masses of atoms, isotopes, and molecules, enabling deeper insights into chemical reactions, molecular structures, and nuclear processes. Its applications extend across multiple fields, from chemistry and physics to biology and environmental science, where it facilitates essential calculations and analyses.

Looking ahead, advancements in technology and measurement techniques will continue to enhance our understanding of atomic mass and isotopic variation, potentially leading to even more refined standards. The atomic mass unit remains a cornerstone of scientific inquiry, enabling discoveries that shape our understanding of the universe at its most fundamental level.

Examples of Atomic Mass Unit Calculations

To illustrate how the atomic mass unit (amu) is used in practice, let’s go through a few examples of typical calculations that involve the amu.

Calculating the Atomic Mass of an Element with Isotopes

Example: Chlorine

Chlorine has two naturally occurring isotopes: chlorine-35 and chlorine-37. The atomic mass of chlorine is calculated as the weighted average of the atomic masses of these two isotopes based on their relative abundance.

• Chlorine-35: Atomic mass = 34.969 amu, Abundance = 75.77%
• Chlorine-37: Atomic mass = 36.966 amu, Abundance = 24.23%

To calculate the average atomic mass of chlorine:

Average Atomic Mass= (34.969×75.77/100)+(36.966×24.23/100) = (26.493)+(8.952)= 35.445amu

Thus, the atomic mass of chlorine is approximately 35.45 amu. This is the value typically listed on the periodic table.

Calculating the Molar Mass of a Compound

Example: Water (H₂O)

Water consists of two hydrogen atoms and one oxygen atom. To find the molar mass of water, we sum the atomic masses of the hydrogen and oxygen atoms.

• Atomic mass of hydrogen (H) = 1.008 amu
• Atomic mass of oxygen (O) = 15.999 amu

The molecular mass of water is:

Molecular Mass of H₂O= (2×1.008)+15.999 = 2.016+15.999 = 18.015 amu

The molar mass of water is, therefore, 18.015 g/mol.

Determining the Number of Atoms in a Sample

Example: A 10-gram sample of carbon (C)

Carbon has an atomic mass of approximately 12.011 amu, and its molar mass is 12.011 g/mol. To determine how many atoms are in a 10-gram sample of carbon, we use Avogadro’s number, which is 6.022×10²³ atoms/mol.

First, calculate the number of moles of carbon in the sample:

Moles of Carbon= 10 g/12.011 g/mol = 0.832 mol

Now, calculate the number of atoms using Avogadro’s number:

Number of Atoms = 0.832 mol × 6.022×10²³ atoms/mol

Number of Atoms=5.01×10²³ atoms

Thus, there are approximately 5.01 × 10²³ atoms in the 10-gram sample of carbon.

Energy Released in a Nuclear Reaction (Mass-Energy Equivalence)

Example: Energy from mass defect in a nuclear reaction

In nuclear reactions, the mass of the products is often slightly less than the mass of the reactants. This difference in mass, known as the “mass defect,” is converted into energy, as described by Einstein’s famous equation E=mc², where E is energy, m is mass, and c is the speed of light.

Assume that in a nuclear reaction, there is a mass defect of 0.001u.

To calculate the energy released:

• 1 amu= 931.494 MeV/c²

Thus, the energy released is:

E= 0.001 u × 931.494 MeV/c² = 0.931MeV

Therefore, the energy released by this mass defect is approximately 0.931 MeV.

Relative Abundance of Isotopes

Example: Calculating the percentage of two isotopes

Let’s say an element has two isotopes, A and B, and their atomic masses are 10 amu and 11 amu, respectively. The average atomic mass of the element is 10.8 amu. If we want to calculate the relative abundance of each isotope, we can set up the following equation:

Let X be the fraction of isotope A, and (1−X) be the fraction of isotope B.

The average atomic mass is given by:

10.8 = (X × 10)+((1−X)×11)

Expanding and simplifying:

10.8 = 10X+11−11X

10.8 = 11-X

Solving for X

X = 11−10.8 = 0.2

Thus, isotope A (10 amu) has a relative abundance of 20%, and isotope B (11 amu) has a relative abundance of 80%.