The Liquid Drop Model (LDM) is a fundamental theoretical framework used to describe the behaviour of atomic nuclei, especially in understanding nuclear fission and fusion processes. It likens the nucleus to a liquid drop, accounting for its bulk properties such as volume, surface tension, and electrostatic repulsion. By addressing the binding energy of the nucleus, this model provides key insights into nuclear stability, radioactive decay, and energy release in nuclear reactions. Though it has limitations, mainly when dealing with light nuclei or detailed shell effects, the model remains pivotal in nuclear physics research and education.
Introduction to the Liquid Drop Model
The Liquid Drop Model (LDM) is a foundational concept in nuclear physics that explains the collective properties of an atomic nucleus. Developed initially by George Gamow and later refined by Niels Bohr and John Archibald Wheeler, this model draws a conceptual parallel between the atomic nucleus and a droplet of liquid. The assumption is that much like molecules in a liquid interact with one another to give rise to the drop’s collective properties, nucleons (protons and neutrons) within the nucleus behave in a similar manner.
This analogy proves particularly useful in explaining large-scale properties of the nucleus, such as its binding energy, nuclear stability, and how it behaves during processes such as nuclear fission and fusion. In this article, we will explore the underlying assumptions, mathematical framework, applications, and limitations of the Liquid Drop Model.
Key Assumptions of the Liquid Drop Model
The LDM rests on several critical assumptions about the behaviour of nucleons within the nucleus:
Bulk Behaviour: The model assumes that the protons and neutrons within a nucleus interact collectively rather than individually, much like molecules in a liquid. This assumption makes it easier to model the nucleus as a whole entity rather than dealing with each nucleon’s behaviour separately.
Short-Range Forces: The strong nuclear force, which holds nucleons together, is assumed to act only over short distances. This is analogous to the cohesive forces between molecules in a liquid, which act primarily between nearest neighbours.
Surface Effects: Much like a liquid droplet, the nucleus experiences surface tension. Nucleons near the surface of the nucleus are not as tightly bound as those in the interior, leading to reduced binding energy for nucleons at the edge.
Electrostatic Repulsion: The electrostatic (Coulomb) repulsion between protons plays a significant role in the behaviour of the nucleus. The repulsive force between the positively charged protons counteracts the attractive strong nuclear force, particularly in larger nuclei with higher number of protons.
Mathematical Framework of the Liquid Drop Model
The energy of the nucleus in the Liquid Drop Model is typically expressed in terms of a semi-empirical mass formula, also known as the Weizsäcker formula or Bethe-Weizsäcker mass formula. This equation estimates the binding energy of a nucleus, accounting for various effects. The formula is as follows:
Eb(Z,A)= αvA – αsA2/3 – αc(Z2/A 1/3) – αα (A-2Z)2/A + δ(A,Z)
Here, the terms represent different physical phenomena:
- Eb(Z,A) is the binding energy of a nucleus with Z protons and A nucleons.
- αvA represents the volume term, proportional to the number of nucleons A, assuming each contributes a roughly constant amount of binding energy.
- αsA2/3 is the surface term, which accounts for the reduction in binding energy for nucleons on the surface of the nucleus due to fewer neighbours.
- αc(Z2/A 1/3) is the Coulomb term, representing the electrostatic repulsion between protons.
- αα (A-2Z)2/A is the asymmetry term, accounting for the fact that nuclei tend to be more stable when the number of protons and neutrons is balanced.
- δ(A,Z) is the pairing term, which accounts for the additional stability of nuclei with even numbers of protons and neutrons.
These terms allow for the calculation of the binding energy of a nucleus, which is a measure of its stability. The larger the binding energy, the more stable the nucleus.
Applications of the Liquid Drop Model
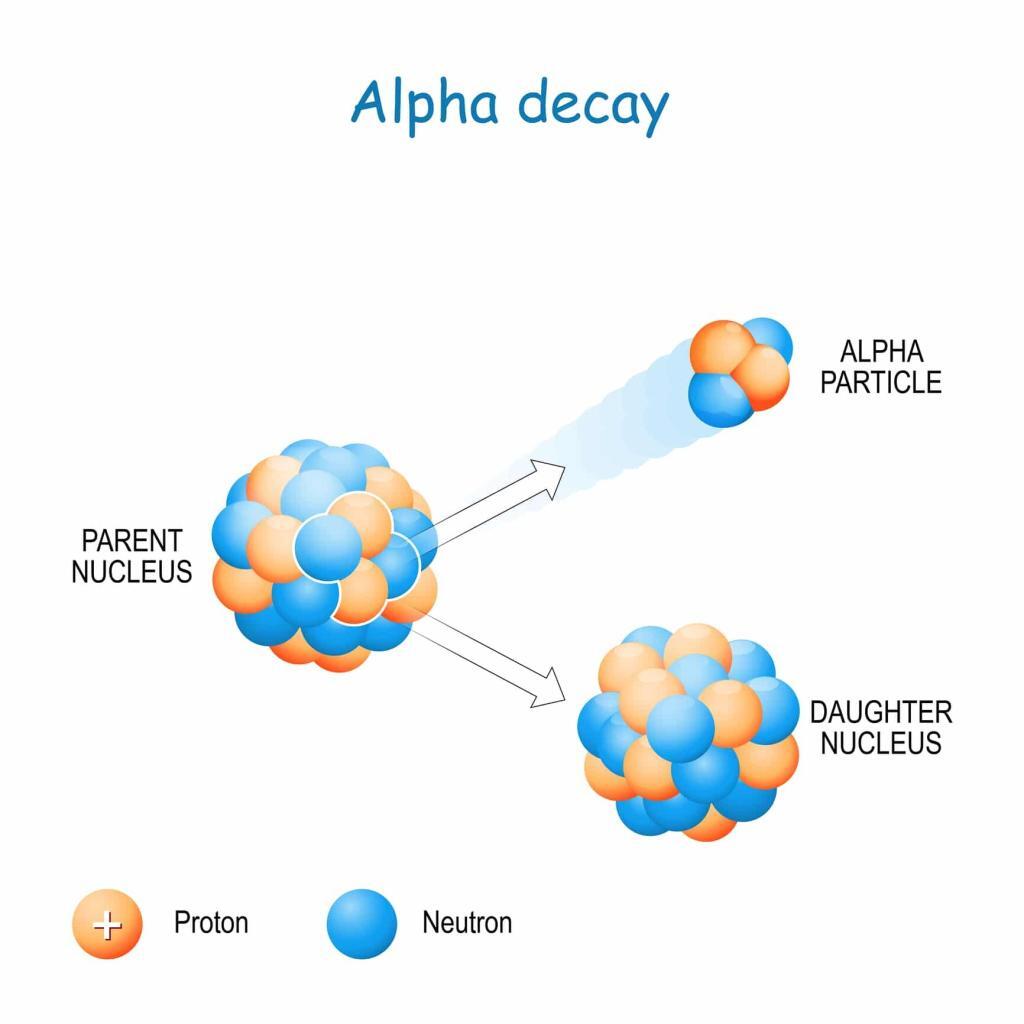
Nuclear Fission: The LDM is crucial for understanding nuclear fission, the process by which a heavy nucleus splits into two or more smaller nuclei. The model explains how the electrostatic repulsion between protons increases as the nucleus becomes larger, eventually overpowering the strong nuclear force and causing the nucleus to split. This insight was pivotal in the development of nuclear reactors and atomic weapons.
Nuclear Fusion: The model also aids in understanding nuclear fusion, where two light nuclei combine to form a heavier nucleus. In fusion, the energy required to overcome the electrostatic repulsion between the protons of the two nuclei must be supplied (usually through extremely high temperatures), after which the strong nuclear force takes over, binding the nuclei together and releasing energy.
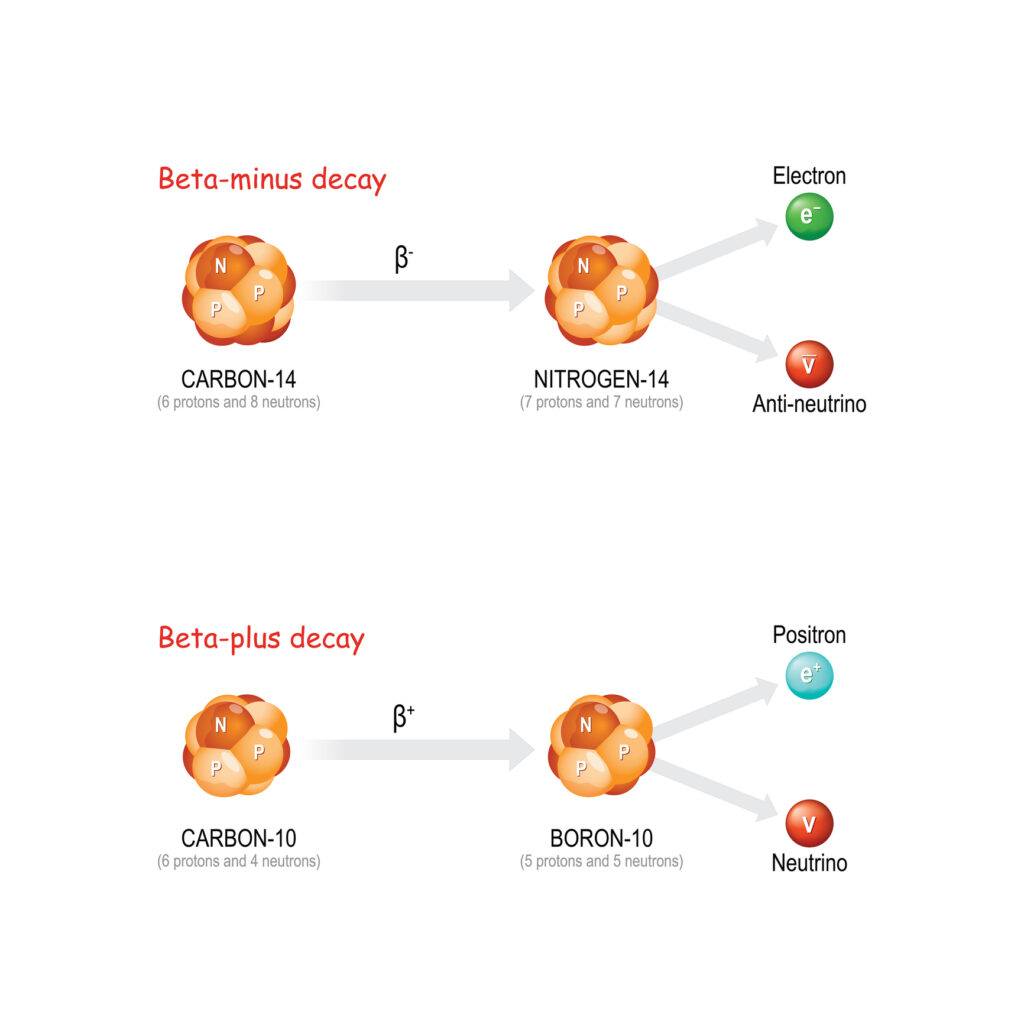
Nuclear Stability and Decay: By using the LDM, physicists can predict which nuclei are more likely to be stable and which will undergo radioactive decay. As described by the asymmetry term in the Weizsäcker formula, the balance between the number of protons and neutrons provides insights into the stability of different isotopes.
Energy Release Calculations: The Liquid Drop Model helps estimate the energy released in both fission and fusion processes. In fission, the resulting fragments of the nucleus have a higher total binding energy than the original nucleus, and the difference is released as energy. In fusion, the binding energy of the new nucleus is also greater than the sum of the initial binding energies of the fusing nuclei, leading to an energy release.
Limitations of the Liquid Drop Model
Although the LDM has been remarkably successful in explaining many nuclear phenomena, it does have some notable limitations:
Shell Effects: The Liquid Drop Model fails to account for the detailed quantum mechanical effects associated with individual nucleons. These effects are crucial for understanding phenomena like the nuclear shell model, which explains the “magic numbers” of nucleons that lead to particularly stable nuclei.
Light Nuclei: The LDM is less accurate when applied to light nuclei, where individual nucleon interactions and quantum effects play a more significant role than collective behaviours.
Pairing Effects: While the pairing term in the Weizsäcker formula accounts for the enhanced stability of nuclei with even numbers of protons and neutrons, it is a rather crude approximation of the underlying quantum mechanical effects. More sophisticated models, such as the nuclear shell model, are needed to fully explain these phenomena.
Deformation and Fission Barriers: In fission processes, the Liquid Drop Model does not fully explain the dynamics of the deformation of the nucleus or the exact nature of the fission barrier. More advanced models are required to describe these processes in detail.
Advancements Beyond the Liquid Drop Model
The Liquid Drop Model laid the groundwork for more sophisticated models in nuclear physics. One such advancement is the nuclear shell model, which takes into account the quantum mechanical behaviour of individual nucleons. In this model, protons and neutrons are arranged in shells, much like electrons in an atom, and nuclei are particularly stable when these shells are filled. The shell model explains phenomena that the Liquid Drop Model cannot, such as why specific nuclei have “magic numbers” of protons or neutrons that make them exceptionally stable.
Another advancement is the collective model, which combines aspects of the Liquid Drop Model with the shell model to explain the rotational and vibrational states of deformed nuclei. This model is particularly useful for understanding the behaviour of medium and heavy nuclei.
Conclusion
The Liquid Drop Model remains a cornerstone of nuclear physics, providing a simple yet powerful way to understand the collective behaviour of nucleons within an atomic nucleus. Its ability to explain nuclear fission, fusion, and the overall stability of nuclei has made it an invaluable tool for scientists working in both theoretical and applied nuclear physics. While it has its limitations, particularly in explaining finer details like shell effects and pairing phenomena, the LDM continues to be a foundational concept that informs more advanced models.
The Liquid Drop Model has significantly shaped our understanding of atomic nuclei and the enormous energy that can be released in nuclear reactions by offering a semi-classical approach to nuclear binding energy and stability. Even in the face of more refined models, its legacy persists as a key milestone in the history of nuclear physics.
You are here: home » medical imaging blog »
