The nuclear shell model is a theoretical framework that explains the structure and behaviour of atomic nuclei in terms of energy levels, much like the electron shell model in atomic physics. This model suggests that nucleons (protons and neutrons) within a nucleus occupy discrete energy levels or “shells.” By understanding these energy levels and their organisation, the shell model has been instrumental in explaining nuclear properties such as stability, magic numbers, and nuclear spins. This article explores the historical development of the nuclear shell model, the concepts of energy levels, the significance of magic numbers, and the model’s applications in both nuclear physics and technology.
Introduction
The study of atomic nuclei has been one of the central endeavours of nuclear physics for over a century. While early nuclear models were primarily concerned with the overall properties of nuclei, the nuclear shell model, introduced in the mid-20th century, provided a deeper understanding of the intricate structure within the nucleus. This model, akin to the shell model for electrons in atoms, describes how protons and neutrons, collectively known as nucleons, are arranged within the nucleus in discrete energy levels. The nuclear shell model has not only helped to explain the stability and properties of specific nuclei but has also led to practical applications in nuclear energy and medical imaging.
Historical Development of the Nuclear Shell Model
The nuclear shell model was developed in the late 1940s by physicists Maria Goeppert Mayer and J. Hans D. Jensen, for which they were awarded the Nobel Prize in Physics in 1963. Before this model, the nucleus was understood mainly through the liquid drop model, which treated the nucleus as a collection of nucleons held together by a force analogous to surface tension in liquids. While the liquid drop model successfully explained some nuclear properties, it failed to account for specific patterns in nuclear stability.
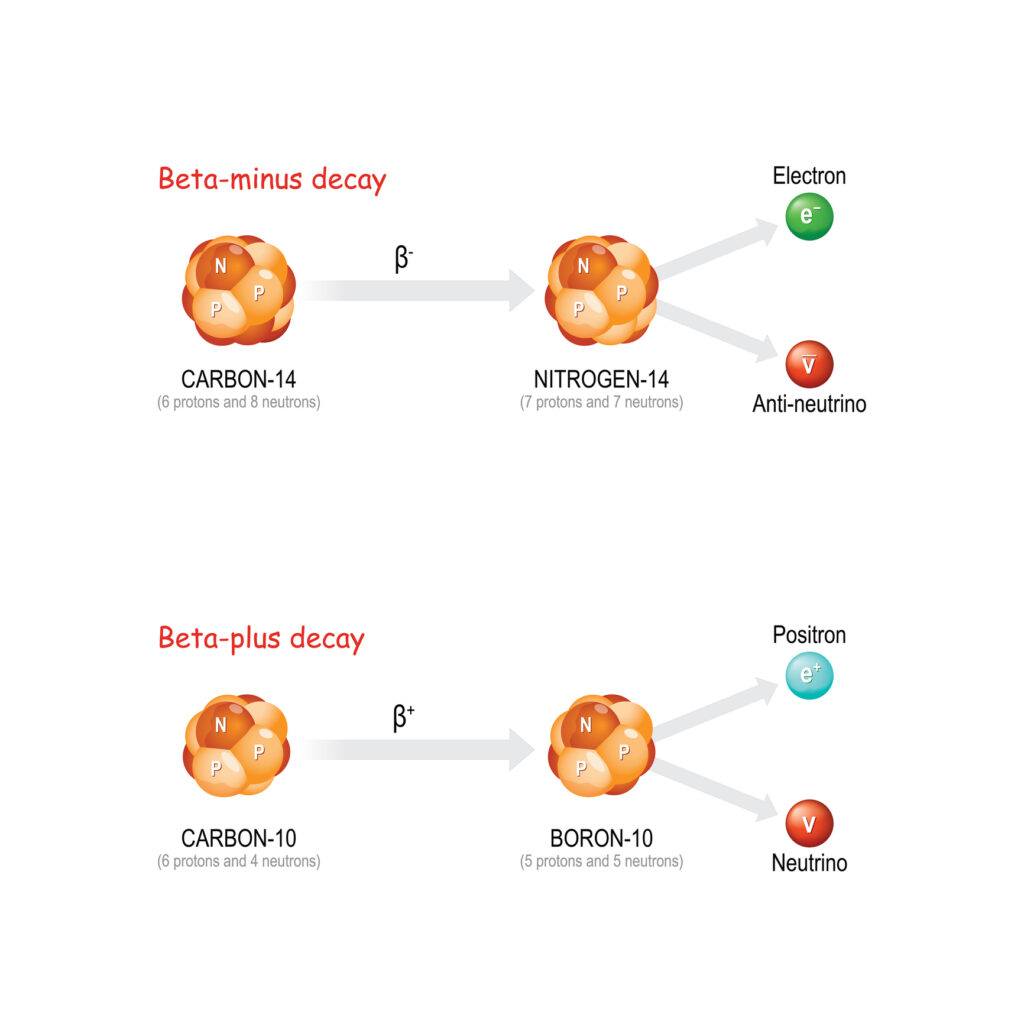
One of the most striking features that the liquid drop model could not explain was the occurrence of “magic numbers,” where nuclei with specific numbers of protons or neutrons were found to be unusually stable. It was through the nuclear shell model that these observations were explained. Goeppert Mayer and Jensen proposed that nucleons in a nucleus, like electrons in an atom, occupy energy levels, and when a shell is filled with nucleons, the nucleus becomes particularly stable. These filled shells correspond to the magic numbers: 2, 8, 20, 28, 50, 82, and 126.
Structure of the Nuclear Shell Model
In the nuclear shell model, nucleons occupy discrete energy levels or “shells,” with each level capable of holding a certain number of protons or neutrons, much like the electron shell model in atomic theory. The arrangement of these energy levels depends on the interplay between the strong nuclear force, which binds nucleons together, and the Pauli exclusion principle, which prevents identical fermions (such as protons or neutrons) from occupying the same quantum state.
The energy levels are derived by solving the Schrödinger equation for a nucleon moving in a potential well, which is typically approximated by a combination of a central potential (representing the overall force holding the nucleons in the nucleus) and a spin-orbit coupling term (which arises from the interaction between a nucleon’s spin and its orbital motion).
Spin-Orbit Coupling
A crucial feature of the nuclear shell model is spin-orbit coupling, which refers to the interaction between a nucleon’s spin and its motion around the nucleus. This interaction causes each energy level to split into two sublevels, one with higher energy and one with lower energy. The strength of the spin-orbit interaction increases with the number of nucleons in the nucleus, leading to more pronounced splitting in heavier nuclei.
Spin-orbit coupling explains the ordering of nuclear energy levels and contributes to the occurrence of magic numbers. When the spin-orbit interaction is taken into account, it becomes clear that certain numbers of protons or neutrons lead to completely filled energy shells, corresponding to particularly stable nuclei.
Magic Numbers and Nuclear Stability
The concept of magic numbers is one of the key successes of the nuclear shell model. These numbers—2, 8, 20, 28, 50, 82, and 126—represent the number of protons or neutrons required to fill a nuclear shell. Nuclei with magic numbers of nucleons exhibit greater stability, as all the available quantum states within a shell are filled, leading to a lower overall energy for the nucleus.
For instance, the nucleus of helium-4, with 2 protons and 2 neutrons, is particularly stable because both the proton and neutron shells are filled. Similarly, lead-208, with 82 protons and 126 neutrons, is a doubly magic nucleus, where both the proton and neutron shells are filled, making it exceptionally stable.
Applications of the Nuclear Shell Model
The nuclear shell model has a wide range of applications in both theoretical and applied physics, including the following areas:
Nuclear Reactions and Decay
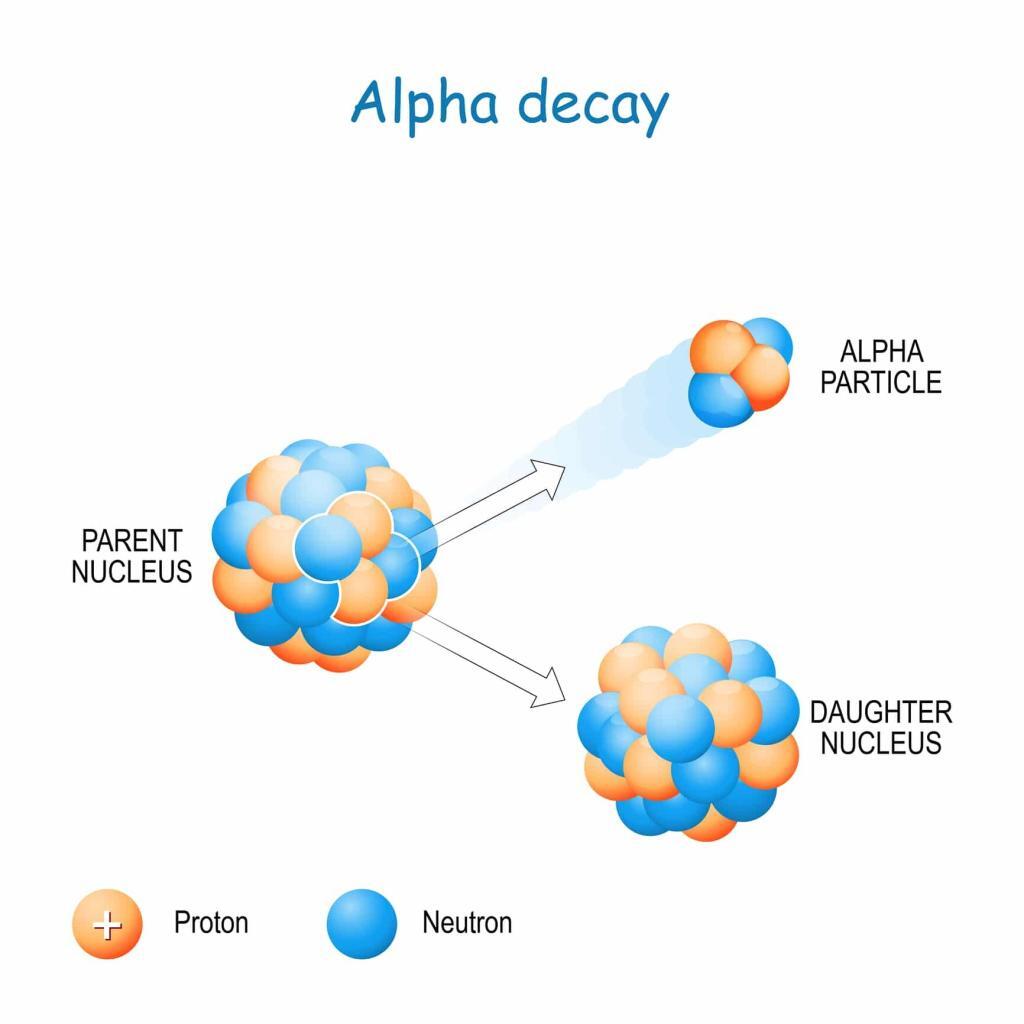
The nuclear shell model provides a framework for understanding nuclear reactions, including fission, fusion, and radioactive decay. In particular, the model helps to explain why certain nuclei are more prone to undergoing decay than others. Nuclei with magic numbers of nucleons are generally more resistant to decay, as they are more stable than nuclei with incomplete shells.
Nuclear Spin and Magnetic Moments
The nuclear shell model also explains the magnetic moments and spins of nuclei. The total spin of a nucleus is determined by the spins of the individual nucleons, which in turn depend on their arrangement within the energy levels. In some cases, nucleons with paired spins cancel each other out, leading to a nucleus with zero total spin. In other cases, the spins of unpaired nucleons combine to give the nucleus a nonzero spin, which can be detected through its magnetic moment.
Isotopes and Nuclear Mass
The isotopes of an element differ in the number of neutrons they contain, and the nuclear shell model helps explain the variations in stability and mass among different isotopes. For example, certain isotopes are more stable than others because their neutron or proton shells are filled, leading to lower overall energy. The mass of a nucleus can also be understood in terms of the binding energy between nucleons, which is affected by the arrangement of protons and neutrons within the shells.
Limitations of the Nuclear Shell Model
While the nuclear shell model has been highly successful in explaining many nuclear properties, it does have its limitations. The model is most effective for describing nuclei near the magic numbers, where the shells are either completely filled or nearly filled. For nuclei with large numbers of unpaired nucleons, or for those far from the magic numbers, the shell model becomes less accurate, and more sophisticated models are required to explain the observed behaviour.
One such model is the collective model, which combines elements of the shell model with features of the liquid drop model to explain the collective motion of nucleons, such as rotations and vibrations of the nucleus as a whole. This model is particularly useful for describing the properties of deformed nuclei, where the simple shell model breaks down.
The Nuclear Shell Model and Modern Physics
Despite its limitations, the nuclear shell model remains a fundamental part of nuclear physics research. Advances in technology, particularly in particle accelerators and detectors, have allowed physicists to test the predictions of the shell model with greater precision. For example, experiments on unstable, short-lived nuclei have revealed new magic numbers that deviate from those predicted by the original model, leading to a deeper understanding of nuclear forces.
The nuclear shell model also plays a crucial role in astrophysics, particularly in the study of stellar nucleosynthesis, the process by which elements are formed in stars. The model helps to explain why certain elements are more abundant in the universe than others and why the production of heavy elements in supernovae follows specific patterns.
Conclusion
The nuclear shell model has provided a powerful framework for understanding the structure and behaviour of atomic nuclei. By treating nucleons as occupying discrete energy levels, the model explains a wide range of nuclear properties, from magic numbers and nuclear stability to the magnetic moments and spins of nuclei. Although the model has its limitations, it has been instrumental in advancing our understanding of nuclear physics and continues to be relevant in modern research.
Applications of the nuclear shell model extend beyond basic science, impacting fields such as nuclear energy, medical imaging, and astrophysics. Its ongoing relevance in both theoretical and applied contexts demonstrates the enduring significance of this foundational model in nuclear physics.
You are here: home » diagnostic medical imaging blog »
